이진탐색트리 - 정의, 삽입, 삭제
2023. 3. 23. 16:18ㆍ자료구조/비선형자료구조
< 개념 >


< 구현 >
// 비선형 자료구조 - 이진 탐색 트리
package binarySearchTree;
import java.util.LinkedList;
import java.util.Queue;
class Node {
int key;
Node left;
Node right;
public Node(int key, Node left, Node right) {
this.key = key;
this.left = left;
this.right = right;
}
}
class BinarySearchTree {
Node head;
BinarySearchTree(int key) {
this.head = new Node(key, null, null);
}
public void addNode(int key) {
if (this.head == null) {
this.head = new Node(key, null, null);
} else {
Node cur = this.head;
while (true) {
Node pre = cur;
if (key < cur.key) { // 삽입하려하는 key값이 현재 가리키는 노드의 키값보다 작으면
cur = cur.left; // 현재 가리키는 노드를 왼쪽으로 가리키도록 함
if (cur == null) { // 옮겨진 현재노드가 비어있다면 그곳에 노드를 추가
pre.left = new Node(key, null, null);
break;
}
} else {
cur = cur.right;
if (cur == null) {
pre.right = new Node(key, null, null);
break;
}
}
}
}
}
public void removeNode(int key) {
Node parent = null; // 부모노드
Node sucessor = null; // 지우려는 대상 노드에 대체할 노드(후계자)
Node predescessor = null; // sucessor의 부모노드
Node child = null; // sucessor의 child가 있는지
Node cur = this.head; // 어떤 노드를 지울 것인지 찾는 노드
while (cur != null) {
if (key == cur.key) {
break;
}
parent = cur;
if (key < cur.key) {
cur = cur.left;
} else {
cur = cur.right;
}
}
if (cur == null) {
System.out.println("key에 해당하는 노드가 없습니다.");
return;
}
if (cur.left == null && cur.right == null) { // 삭제하려는 노드가 leaf노드이고
if (parent == null) { // 삭제하려는 노드가 root노드일 때,
this.head = null;
} else { // 삭제하려는 노드가 level1 이후일 때,
if (parent.left == cur) {
parent.left = null;
} else {
parent.right = null;
}
}
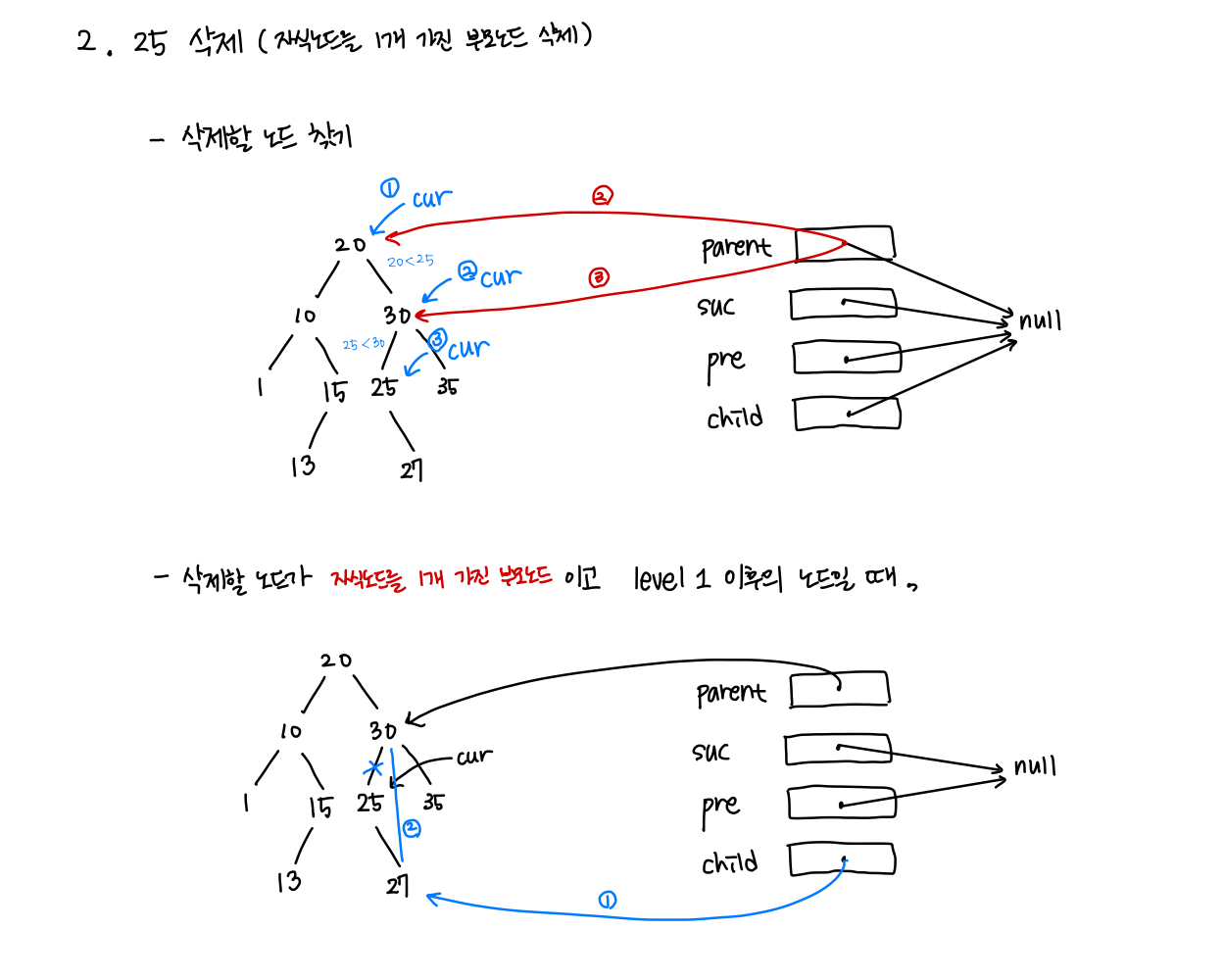
} else if ((cur.left != null && cur.right == null) || (cur.left == null && cur.right != null)) { // 삭제하려는 노드가 자식노드를 한 개 가진 부모노드일 때,
// 삭제하려는 노드의 자식노드 가리키기
if (cur.left != null) {
child = cur.left;
} else {
child = cur.right;
}
if (parent == null) { // 삭제하려는 노드가 root노드일 때,
this.head = child;
} else { // 삭제하려는 노드가 level1 이후일 때,
// 삭제하려는 도느의 부모노드에서 삭제하려는 노드의 자식노드를 연결하기
if (parent.left == cur) {
parent.left = child;
} else {
parent.right = child;
}
}
} else { // 자식 노드가 둘일 때,
// 좌측 서브트리에서 가장 큰 노드 찾기
sucessor = cur.left;
predescessor = cur;
while (sucessor.right != null) {
predescessor = sucessor;
sucessor = sucessor.right;
}
predescessor.right = sucessor.left;
// 현재노드 위치에 왼쪽 서브트리에서 제일 큰 노드로 변경
sucessor.left = cur.left;
sucessor.right = cur.right;
if (parent == null) {
this.head = sucessor;
} else {
if (parent.left == cur) {
parent.left = sucessor;
} else {
parent.right = sucessor;
}
}
}
}
public void levelOrder(Node node) {
/*
아이디어: A를 큐에 삽입. A를 꺼내 출력 및 A의 왼쪽(B), 오른쪽(C) 자식 노드가 있다면 그들을 큐에.
큐의 poll()로 B의 왼쪽, 오른쪽 자식 노드가 있다면 큐에 삽입. C마찬가지... 반복
*/
Queue<Node> queue = new LinkedList();
queue.add(node); // root 노드
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.print(cur.key + " ");
if (cur.left != null) {
queue.offer(cur.left); // == add
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
System.out.println();
}
}
public class binarySearchTreeClass {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree(20);
bst.addNode(10);
bst.addNode(30);
bst.addNode(1);
bst.addNode(15);
bst.addNode(25);
bst.addNode(13);
bst.addNode(35);
bst.addNode(27);
bst.addNode(40);
bst.levelOrder(bst.head);
bst.removeNode(40);
bst.levelOrder(bst.head);
bst.removeNode(25);
bst.levelOrder(bst.head);
bst.removeNode(20);
bst.levelOrder(bst.head);
}
}
- 설명
BinarySearchTree bst = new BinarySearchTree(20);
bst.addNode(10);
bst.addNode(30);
bst.addNode(1);
bst.addNode(15);
bst.addNode(25);
bst.addNode(13);
bst.addNode(35);
bst.addNode(27);
bst.addNode(40);
bst.levelOrder(bst.head);
bst.removeNode(40);
bst.levelOrder(bst.head);
bst.removeNode(25);
bst.levelOrder(bst.head);
bst.removeNode(20);
bst.levelOrder(bst.head);




< 재귀로 구현 >
// 앞의 BST 삽입, 삭제 코드를 재귀 형태로 구현
package binarySearchTree;
import java.util.LinkedList;
import java.util.Queue;
class BinarySearchTree2 {
Node head;
BinarySearchTree2(int key) {
this.head = new Node(key, null, null);
}
public Node addNodeRecursive(Node cur, int key) {
// 탈출조건
if (cur == null) {
return new Node(key, null, null);
}
if (key < cur.key) {
cur.left = addNodeRecursive(cur.left, key);
} else {
cur.right = addNodeRecursive(cur.right, key);
}
return cur;
}
public Node removeNodeRecursive(Node cur, int key) {
// 탈출조건
if (cur == null) {
return null;
}
if (key < cur.key) {
cur.left = removeNodeRecursive(cur.left, key);
} else if (key > cur.key) {
cur.right = removeNodeRecursive(cur.right, key);
} else {
if (cur.left == null) { // 자식노드가 하나이거나 없는 경우
return cur.right;
} else if (cur.right == null) { // 자식노드가 하나이거나 없는 경우
return cur.left;
} else { // 자식노드 둘 다 존재할 때
Node predecessor = cur;
Node successor = cur.left;
while (successor.right != null) {
predecessor = successor;
successor = successor.right;
}
predecessor.right = successor.left;
cur.key = successor.key;
}
}
return cur;
}
public void levelOrder(Node node) {
/*
아이디어: A를 큐에 삽입. A를 꺼내 출력 및 A의 왼쪽(B), 오른쪽(C) 자식 노드가 있다면 그들을 큐에.
큐의 poll()로 B의 왼쪽, 오른쪽 자식 노드가 있다면 큐에 삽입. C마찬가지... 반복
*/
Queue<Node> queue = new LinkedList();
queue.add(node); // root 노드
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.print(cur.key + " ");
if (cur.left != null) {
queue.offer(cur.left); // == add
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
System.out.println();
}
}
public class changeBST {
public static void main(String[] args) {
BinarySearchTree2 bst = new BinarySearchTree2(20);
bst.head = bst.addNodeRecursive(bst.head, 30);
bst.head = bst.addNodeRecursive(bst.head,1);
bst.head = bst.addNodeRecursive(bst.head,15);
bst.head = bst.addNodeRecursive(bst.head,25);
bst.head = bst.addNodeRecursive(bst.head,13);
bst.head = bst.addNodeRecursive(bst.head,35);
bst.head = bst.addNodeRecursive(bst.head,27);
bst.head = bst.addNodeRecursive(bst.head,40);
bst.levelOrder(bst.head);
bst.head = bst.removeNodeRecursive(bst.head, 40);
bst.levelOrder(bst.head);
bst.head = bst.removeNodeRecursive(bst.head, 25);
bst.levelOrder(bst.head);
bst.head = bst.removeNodeRecursive(bst.head, 20);
bst.levelOrder(bst.head);
}
}
'자료구조 > 비선형자료구조' 카테고리의 다른 글
| 힙 (0) | 2023.03.24 |
|---|---|
| 이진탐색트리 - AVL Tree (0) | 2023.03.23 |
| 트리 (0) | 2023.02.25 |